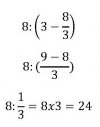Le sfide mentali ...

[cri1401]

Io ho letto la soluzione online ma non danno spiegazioni di come ci sono arrivati

 

[cri1401]

Guardandola ho capito ed è simile a quella di @ironbee semplicemente senza lo 0.

 

[Amy]

Allora andrebbe bene anche (3x8)+(3x8)/2
Sarebbe troppo semplice.
La soluzione cmq c'è usando solo due volte 8 e due volte 3. Senza altri numeri di mezzo.
Non la dico perché l'ho letta in rete

Cmq nell'immagine del gioco ci sono anche i due esempi.

Io non conosco tutte queste cose spiegate da Amy, magari ha ragione e nel gioco non l'hanno spiegato alla perfezione, ma secondo me le regole erano chiare

no, fa 24 + 12 = 36 ....
leggerla in rete non vale .... sono le nostre sfide mentali, se ci arriviamo bene se andiamo a guardare è barare.

Ironbee ha letto esattamente quello che c'è scritto nel testo.
Aggiungere un solo significa aggiungere una regola del gioco che non c'è.
indipendentemente dal fatto che esista anche una soluzione con solo 3, 3, 8, 8.

E adesso vale la sfida di @Angil e @Picantina : visto che la soluzione c'è aggiungendo la limitazione dei soli 3 e 8 tocca a noi trovarla e spiegarla ... ma senza guardare in rete.
Alla caricaaaaa ....

 

[Angil]

no, fa 24 + 12 = 36 ....
leggerla in rete non vale .... sono le nostre sfide mentali, se ci arriviamo bene se andiamo a guardare è barare.

Ironbee ha letto esattamente quello che c'è scritto nel testo.
Aggiungere un solo significa aggiungere una regola del gioco che non c'è.
indipendentemente dal fatto che esista anche una soluzione con solo 3, 3, 8, 8.

E adesso vale la sfida di @Angil e @Picantina : visto che la soluzione c'è aggiungendo la limitazione dei soli 3 e 8 tocca a noi trovarla e spiegarla ... ma senza guardare in rete.
Alla caricaaaaa ....

Va beh, era giusto un esempio al volo e ho sbagliato le parentesi, avrebbe dovuto essere (3×8+3×8)÷2

Certo, ho letto in rete perché non ho trovato la soluzione per mia capacità e ovviamente non partecipo

 

[cri1401]

Se volete la pubblico

 

[Amy]

Metti anche un'altra sfida.

 

[cri1401]

Metti anche un'altra sfida.

vedo se ne trovo una

La soluzione l'ho trovata qui
e qui ve l'ho sviluppata: ieri ci ho provato diverse volte, trovandone anche di uguali alle vostre, ma dopo diversi tentativi di equazioni ho rinunciato

 

[erilla]

In questo indovinello non importa trovare una soluzione 'giusta'; quello che occorre è trovare una soluzione plausibile, cioè che rispetti e spieghi tutte le condizioni poste dalla storia: la tengo corta ed essenziale.
Un uomo abita al 10° piano di un palazzo.
Ogni mattina prende l'ascensore, scende e va al lavoro; ogni sera torna a casa, prende l'ascensore e ...
se è da solo e le previsioni del tempo davano 'bel tempo' allora arriva fino al 7° piano e fa gli ultimi 3 piani a piedi,
se è in compagnia di una qualsiasi persona arriva fino al 10° con l'ascensore,
se era prevista pioggia per quella giornata arriva fino al 10° piano con l'ascensore.
Come si psiega questo suo strano comportamento?

Se c'è bello va al lavoro a piedi, indossa delle scarpe comode e al ritorno si fa gli ultimi 3 piani di corsa per fare anche un po' di "step", se invece incontra qualcuno in ascensore gli piace socializzare e non pensa più all'attività fisica, se piove usa le galosce e l'ombrello che non gli permettono di fare agevolmente gli ultimi 3 piani a piedi di corsa.

 

[Amy]

Grazie @erilla hai trovato un'altra soluzione plausibile (rispetta tutte le condizioni poste) penso proprio che ti ruberò l'idea quando userò questo indovinello

In questo indovinello non importa trovare una soluzione 'giusta'; quello che occorre è trovare una soluzione plausibile, cioè che rispetti e spieghi tutte le condizioni poste dalla storia: la tengo corta ed essenziale.
Un uomo abita al 10° piano di un palazzo.
Ogni mattina prende l'ascensore, scende e va al lavoro; ogni sera torna a casa, prende l'ascensore e ...
se è da solo e le previsioni del tempo davano 'bel tempo' allora arriva fino al 7° piano e fa gli ultimi 3 piani a piedi,
se è in compagnia di una qualsiasi persona arriva fino al 10° con l'ascensore,
se era prevista pioggia per quella giornata arriva fino al 10° piano con l'ascensore.
Come si psiega questo suo strano comportamento?

io mi ricordo quella dell'uomo basso per arrivare al tasto del 10° piano, quindi o si faceva una parte di piani a piedi, o si faceva schiacciare il tasto da chi era con lui o usava l'ombrello

Se c'è bello va al lavoro a piedi, indossa delle scarpe comode e al ritorno si fa gli ultimi 3 piani di corsa per fare anche un po' di "step", se invece incontra qualcuno in ascensore gli piace socializzare e non pensa più all'attività fisica, se piove usa le galosce e l'ombrello che non gli permettono di fare agevolmente gli ultimi 3 piani a piedi di corsa.

 

[Harma]

Rimango sintonizzata.....

 

[Amy]

 

[Amy]

geometria ... @cri1401 , criiiii.
non vale cercare la soluzione in internet .... ma l'uso di un cad lo consideriamo valido?????
motivare la risposta

 

[cri1401]

L'unica cosa che mi viene in mente è che 100 è la radice quadrata di 10000

 

[Amy]

L'unica cosa che mi viene in mente è che 100 è la radice quadrata di 10000

in effetti ... è una barzelletta matematica lo humor dei matematici è tremendo

 

[Amy]

geometria ... @cri1401 , criiiii.
non vale cercare la soluzione in internet .... ma l'uso di un cad lo consideriamo valido?????
motivare la risposta
Vedi l'allegato 684306

Anche qui non c'è scritto che il triangolo deve essere equilatero (vedi discussione sulla soluzione di @ironbee)
io ho visto una possibile soluzione in internet e mi taccio

 

[Amy]

e ho trovato nel sito suggerito da @cri1401 un altro giochino questa volta numerico:

Trovate un numero di 10 cifre in cui la prima cifra sia il numero degli 0 presenti nel numero, la seconda cifra sia il numero di 1 presenti nel numero, le terza cifra sia il numero di 2 presenti nel numero e così via .... fino alla decima cifra che è il numero di 9 presenti nel numero.

 

[ironbee]

e ho trovato nel sito suggerito da @cri1401 un altro giochino questa volta numerico:

Trovate un numero di 10 cifre in cui la prima cifra sia il numero degli 0 presenti nel numero, la seconda cifra sia il numero di 1 presenti nel numero, le terza cifra sia il numero di 2 presenti nel numero e così via .... fino alla decima cifra che è il numero di 9 presenti nel numero.

6210001000 mi pare sia conforme alla definizione. Sono andato per tentativi, non so se c'è un metodo più matematico.

 

[ironbee]

geometria ... @cri1401 , criiiii.
non vale cercare la soluzione in internet .... ma l'uso di un cad lo consideriamo valido?????
motivare la risposta
Vedi l'allegato 684306

Se il triangolo di partenza non deve essere necessariamente equilatero, una soluzione potrebbe essere questa: (la descrivo perché non so come disegnare con il telefono):
disegnate un rettangolo con i lati uno il doppio dell'altro, tracciate la diagonale e avrete due triangoli, aggiungete un triangolo sopra e uno di fianco al rettangolo di partenza e il quinto dall'altra parte, ruotato di 90 gradi.

 

[Amy]

Se il triangolo di partenza non deve essere necessariamente equilatero, una soluzione potrebbe essere questa: (la descrivo perché non so come disegnare con il telefono):
disegnate un rettangolo con i lati uno il doppio dell'altro, tracciate la diagonale e avrete due triangoli, aggiungete un triangolo sopra e uno di fianco al rettangolo di partenza e il quinto dall'altra parte, ruotato di 90 gradi.

Mi piace la tua soluzione.

mi ricorda la storia dell'imperatore cinese che si era innamorato del colore di un vaso; aveva promesso una ricchezza enorme a colui che avesse ridipinto la sua stanza da letto dello stesso colore del vaso e il taglio della testa a coloro che avessero fallito.
Molti pittori ci lasciarono il collo per non essere riusciti a riprodurre alla perfezione la tonalità del vaso tanto era bella e particolare.
Hu xin Jin era un bravo e sveglio pittore e volle provare: chiese al sovrano di avere a disposizione un tempo illimitato e si chiuse nella stanza da solo e con tanti colori; poteva aprire la porta e chiamare i servitori del re nel caso avesse avuto bisogno di qualcosa.
Per un mese intero Hu Xin Jin fece tentativi su tentativi ma trovare quella particolare tonalità che piaceva tanto al re sembrava impossibile.
Nello stesso modo passò il secondo mese.
Alla fine del terzo mese Hu Xin Jin apri la porta, chiamò un servitore e fece chiamare il re. La stanza era pronta.
Il re fu sodisfatto del lavoro e Hu Xin Jin divenne ricchissimo.

Come ha fatto ad avere successo?

Il nome del pittore è inventato (fosse mai che un altro Hu Xin Jin legga proprio questo post e decida di )

 

[Amy]

6210001000 mi pare sia conforme alla definizione. Sono andato per tentativi, non so se c'è un metodo più matematico.

non è vietato andare per tentativi ... i puristi matematici lo considerano 'poco elegante' ma ...
la tua soluzione rispecchia le richieste.
Ora, in teoria, dovresti spiegare come ci sei arrivato.