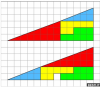
Non avevo capito volessi una dimostrazione matematica allora:
Calcolando trigonometricamente gli angoli del triangolo rosso abbiamo 22,02-90-67,98
Mentre gli angoli di quello azzurro risultano essere 23,57-90-66,47
Assemblando le figure si formano due quadrilateri, il primo (concavo) ha come angoli 22.02-181.55-66,47-90
E il secondo 23,57-178,49-67,98-90
Come si vede sia 181.55 sia 178.49 sono simili all'angolo piatto e ciò inganna l'occhio, ma essendo due poligoni differenti hanno due aree differenti e questa differenza corrisponde a quel quadratino mancante
Comunque si vedeva a occhio:LOL::LOL::LOL:

 :LOL:
:LOL: non mi sono messa a calcolare gli angoli
non mi sono messa a calcolare gli angoli





